Generating non-repeating (unique) random numbers in JavaScript
While working on my hobby project Is this your card, I needed to have a list of unique (non-repeated) random numbers in JavaScript. Of course my first thought was to use the JS's Math.random().
Math.random()
Calling Math.random() will return a number between between 0 (inclusive), and 1 (exclusive). Let's call it for 10 times and see what happens.
We got 10 float random numbers. Let's get rid of those unsightly extra decimals. First multiply the random numbers by 10.
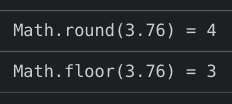
Math.random() * 10;This will give us the random values ranging from 0 (inclusive) to 10 (exclusive). Just to get the idea multiplying with 100 with will result in random numbers ranging from 0 (inclusive) to 100 (exclusive). Now we can get rid of the decimals completely by using Math.floor() or Math.round(). Math.floor(num) will round down the value of num while Math.round(num) will round up the value of num.
If we use Math.floor() for Math.random() * 10;, we will get the range of [ 0 to 9]. For Math.round() we will get [ 1 to 10]. For simplicity sake, let's just use the Math.floor()

We can already see some numbers are repeated. A dirty solution would be to check if the generated number already exists before pushing it to the array. This is a bad solution as we need to iterate through array every time we want to add a number. It would be fine for a small scale of numbers, but it will become a big problem for a large scale of numbers. It will work for my project, but I don't want a workaround for my project.
So I explored further, reading through StackOverflow questions and googling. And I found this post by Mike Bostock. I realize one way to get what I want is to generate the numbers in the order first then shuffle them 💡. In this case, by using Fisher–Yates shuffle.
// populate numbers
for (let i = 0; i < total; i++) {
numArray.push(i);
}
Fisher-Yates shuffle
According to Wikipedia. "The Fisher-Yates shuffle effectively puts all the elements into a hat; it continually determines the next element by randomly drawing an element from the hat until no elements remain." What does it mean for us? It means we will loop through the array once. Let me break it down in steps so that it would be easier to understand.
Step 1 : start index from 0 (you may start from index = len-1 as well. More explanation at the end).
Step 2 : pick a random number from the remaining values. Range to choose is from index+1 , to length - index - 1. For our case the range is from 1 to 9 both inclusive. In the image below, the index to swap, coincidentally, is index 1.
Ste 3 : swap the number from current index with the random number picked at Step 2. repeat.
See the full action below. There were some cases where index and swap index are the same. Something I need to improve on my random selection. But this should give you a good idea of how generate unique random numbers.

Note: I animated using Framer motion for this gif. You may check the sandbox here
The finished implementation of the generating non-repeated randoms should look like this.
for (let index = 0; index < TOTAL_CARDS - 1; index++) {
let maxIndex = TOTAL_CARDS - 1;
let minIndex = index + 1;
let swapIndex = Math.floor(Math.random() * (maxIndex - minIndex)) + minIndex;
let tmp = col[index];
col[index] = col[swapIndex];
col[swapIndex] = tmp;
}We can see from the code above that getting the random index is a bit complicated. We can simplify this if we traverse the array starting from the highest index. In fact, this is the way most people (including Mike Bostock) implements the shuffle. Let see what it looks like.
for (let j = TOTAL_CARDS - 1; j >= 0; j--) {
let swapIndex = Math.floor(Math.random() * j);
let tmp = col[swapIndex];
col[swapIndex] = col[j];
col[j] = tmp;
}See! This is much simpler and easier to understand. Thank you for checking out my blog. I hope you learnt something. Please leave a comment if you have any questions or if you see some mistakes in my post.